সমমিতীয় উপস্থাপন

সমমিতীয় উপস্থাপন (ইংৰাজী: Isometric projection) হৈছে কাৰিকৰী আৰু অভিযান্ত্ৰিক অংকনত ত্ৰিমাত্ৰিক বস্তুক দুটা মাত্ৰাত দৃশ্যমানভাৱে প্ৰতিনিধিত্ব কৰাৰ এক পদ্ধতি। ই এটা এক্সন’মেট্ৰিক প্ৰক্ষেপণ য’ত তিনিটা স্থানাংক অক্ষ সমানে আগলৈ চুটি হোৱা দেখা যায় আৰু ইয়াৰে যিকোনো দুটাৰ মাজৰ কোণ ১২০ ডিগ্ৰী।

অৱলোকন

ঘনক এটাৰ সমমিত অংকন

এই দৃষ্টিভংগী লাভ কৰিবলৈ কেমেৰাৰ ঘূৰণৰ প্ৰয়োজন হৈছিল

"আইছ’মেট্ৰিক'" শব্দটো গ্ৰীক ভাষাৰ পৰা আহিছে যাৰ অৰ্থ হৈছে "সমান পৰিমাপ", ইয়াৰ দ্বাৰা প্ৰতিফলিত হয় যে প্ৰক্ষেপণৰ প্ৰতিটো অক্ষৰ কাষৰে স্কেল একে।

x, y, আৰু z অক্ষৰ প্ৰক্ষেপণৰ মাজৰ কোণবোৰ সকলো একে বা ১২০° হোৱাকৈ চোৱাৰ দিশটো বাছি লৈ বস্তু এটাৰ সমমিতি দৃশ্য লাভ কৰিব পাৰি। উদাহৰণস্বৰূপে, ঘনক এটাৰ সহায়ত প্ৰথমে পোনে পোনে এটা মুখৰ ফালে চাই এই কাম কৰা হয়। ইয়াৰ পিছত ঘনকটোক উলম্ব অক্ষৰ চাৰিওফালে ±৪৫° ঘূৰোৱা হয়, তাৰ পিছত অনুভূমিক অক্ষৰ চাৰিওফালে প্ৰায় ৩৫.২৬৪° (ঠিক আৰ্কচিন ^১⁄_√৩ বা আৰ্কটান ¹⁄_√২, যিটো মেজিক কোণৰ সৈতে জড়িত) ঘূৰোৱা হয়। ঘনকটোৰ সৈতে (চিত্ৰ চাওক) ফলাফলৰ ২ডি অংকনৰ পৰিধি এটা নিখুঁত নিয়মিত ষড়ভুজ: সকলো ক'লা ৰেখাৰ দৈৰ্ঘ্য সমান আৰু ঘনকটোৰ সকলো মুখৰ ক্ষেত্ৰফল একে। আইছ’মেট্ৰিক গ্ৰাফ পেপাৰ এটা সাধাৰণ অংকন কাগজৰ তলত ৰাখিব পাৰি যাতে গণনা অবিহনেই ইয়াৰ প্ৰভাৱ লাভ কৰাত সহায় হয়।

একেদৰেই ত্ৰিমাত্ৰিক দৃশ্যত আইছ’মেট্ৰিক দৃশ্য লাভ কৰিব পাৰি। মজিয়াৰ সমান্তৰালভাৱে প্ৰান্তিককৃত আৰু স্থানাংক অক্ষৰ সৈতে প্ৰান্তিককৃত কেমেৰাৰ পৰা আৰম্ভ কৰি ইয়াক প্ৰথমে অনুভূমিকভাৱে (উলম্ব অক্ষৰ চাৰিওফালে) ±৪৫°, তাৰ পিছত অনুভূমিক অক্ষৰ চাৰিওফালে ৩৫.২৬৪° ঘূৰাই দিয়া হয়।

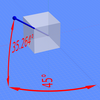
সমমিতি প্ৰক্ষেপণক দৃশ্যমান কৰিব পৰা আন এটা উপায় হ'ল ওপৰৰ চুক এটাৰ পৰা আৰম্ভ কৰি বিপৰীত, তলৰ চুকটোৰ ফালে চাই ঘনকীয় কোঠাৰ ভিতৰৰ দৃশ্য এটা বিবেচনা কৰা। x-অক্ষটো তিৰ্যকভাৱে তললৈ আৰু সোঁফালে, y-অক্ষটো তিৰ্যকভাৱে তললৈ আৰু বাওঁফালে আৰু z-অক্ষটো পোনকৈ ওপৰলৈ বিস্তৃত। ছবিখনত উচ্চতাৰ দ্বাৰাও গভীৰতা দেখুওৱা হৈছে। অক্ষৰ কাষেৰে অংকন কৰা ৰেখাবোৰ ইটোৱে সিটোৰ লগত ১২০° ত থাকে।

এই সকলোবোৰ ক্ষেত্ৰতে, সকলো এক্সন'মেট্ৰিক আৰু অৰ্থ'গ্ৰাফিক প্ৰজেকচনৰ দৰেই, এনে কেমেৰা এটাক বস্তু-স্থান টেলিচেণ্ট্ৰিক লেন্সৰ প্ৰয়োজন হ'ব, যাতে কেমেৰাৰ পৰা দূৰত্বৰ লগে লগে প্ৰক্ষেপিত দৈৰ্ঘ্য সলনি নহয়।

"আইছ'মেট্ৰিক" শব্দটো প্ৰায়ে ভুলকৈ এক্সন'মেট্ৰিক প্ৰক্ষেপণক বুজাবলৈ ব্যৱহাৰ কৰা হয়, সাধাৰণতে। কিন্তু প্ৰকৃততে এক্সন’মেট্ৰিক প্ৰক্ষেপণ তিনি ধৰণৰ: সমমিতি, ডাইমেট্ৰিক আৰু তিৰ্যক।

ঘূৰ্ণনৰ কোণ

সমমিতি প্ৰক্ষেপণৰ বাবে প্ৰয়োজনীয় দুটা কোণৰ পৰা দ্বিতীয়টোৰ মানটো বিপৰীতমুখী যেন লাগিব পাৰে। প্ৰথমে এটা ঘনক কল্পনা কৰি ইয়াৰ কাষ দুটাৰ দৈৰ্ঘ্য ২ একক ল'লে, আৰু ইয়াৰ কেন্দ্ৰ অক্ষৰ উৎপত্তিস্থলত বুলি ধৰিলে, ইয়াৰ সকলো মুখমণ্ডলে উৎপত্তিস্থলৰ পৰা ১একক দূৰত্বত অক্ষবোৰক ছেদ কৰিব। পাইথাগোৰাছৰ উপপাদ্য ব্যৱহাৰ কৰি আমি ৰেখাডালৰ কেন্দ্ৰৰ পৰা যিকোনো প্ৰান্তৰ মাজলৈকে √২ হিচাপে গণনা কৰিব পাৰো। x-অক্ষত ঘনকটোক ৪৫° ঘূৰাই দিলে (১, ১, ১) বিন্দুটো সেয়েহে ডায়াগ্ৰামত দেখুওৱাৰ দৰে (১, ০, √২) হ’ব। দ্বিতীয় ঘূৰ্ণনৰ লক্ষ্য হৈছে ধনাত্মক z-অক্ষত একেটা বিন্দু অনা আৰু সেয়েহে ¹⁄_√২ ৰ চাপস্পৰ্শকৰ সমান মানৰ ঘূৰ্ণন কৰিব লাগিব যিটো প্ৰায় ৩৫.২৬৪°।

গণিত

আইছ’মেট্ৰিক দৃশ্য লাভ কৰিবলৈ আঠটা ভিন্ন অভিমুখীতা থাকা প্ৰয়োজন, সেয়া নিৰ্ভৰ কৰে দৰ্শকে কোনটো অক্টেণ্টত চায়। ত্ৰিমাত্ৰিক স্থানত এটা বিন্দু a_x,y,zৰ পৰা প্ৰথম অক্টেণ্টটোলৈ চাই ২ডি স্থানত এটা বিন্দু b_x,yলৈ সমমিতীয় ৰূপান্তৰ ঘূৰ্ণন মেট্ৰিস্কৰ সহায়ত গাণিতিকভাৱে এইদৰে লিখিব পাৰি: $${\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&{\cos \alpha }&{\sin \alpha }\\0&{-\sin \alpha }&{\cos \alpha }\\\end{bmatrix}}{\begin{bmatrix}{\cos \beta }&0&{-\sin \beta }\\0&1&0\\{\sin \beta }&0&{\cos \beta }\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}={\frac {1}{\sqrt {6}}}{\begin{bmatrix}{\sqrt {3}}&0&-{\sqrt {3}}\\1&2&1\\{\sqrt {2}}&-{\sqrt {2}}&{\sqrt {2}}\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}$$

য’ত α = arcsin(tan ৩০°) ≈ ৩৫.২৬৪° আৰু β = ৪৫°। ওপৰত ব্যাখ্যা কৰা অনুসৰি, এইটো হৈছে উলম্ব (ইয়াত y) অক্ষৰ চাৰিওফালে β দ্বাৰা ঘূৰ্ণন, তাৰ পিছত অনুভূমিক (ইয়াত x) অক্ষৰ চাৰিওফালে α দ্বাৰা ঘূৰ্ণন। ইয়াৰ পিছত xy-সমতললৈ এটা অৰ্থগ্ৰাফিক প্ৰক্ষেপণ কৰা হয়: $${\begin{bmatrix}\mathbf {b} _{x}\\\mathbf {b} _{y}\\0\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}$$

আন ৭টা সম্ভাৱনা হয় বিপৰীত ফালে ঘূৰি বা এয়া নহ'বও পাৰে, আৰু তাৰ পিছত দৃশ্যৰ দিশ ওলোটা কৰি বা নকৰাকৈ পোৱা যায়।

ইতিহাস

প্ৰথমবাৰৰ বাবে অধ্যাপক উইলিয়াম ফেৰিছে (১৭৫৯–১৮৩৭) আনুষ্ঠানিকভাৱে প্ৰদান কৰা সমমিতিৰ ধাৰণাটো শতিকাজুৰি মোটামুটি অভিজ্ঞতাভিত্তিক ৰূপত বিদ্যমান আছিল। ১৯ শতিকাৰ মাজভাগৰ পৰা সমমিতি "অভিযন্তাসকলৰ বাবে এক অমূল্য আহিলাত পৰিণত হয় আৰু তাৰ কিছু সময়ৰ পিছতে ইউৰোপ আৰু আমেৰিকাৰ স্থাপত্য প্ৰশিক্ষণ পাঠ্যক্ৰমৰ পাঠ্যক্ৰমত এক্স'ন'মেট্ৰি আৰু সমমিতি অন্তৰ্ভুক্ত কৰা হয়।" জান ক্ৰিকে (২০০০)ৰ মতে কিন্তু "এক্স'ন'মেট্ৰিৰ উৎপত্তি চীনত হৈছিল। চীনা শিল্পত ইয়াৰ কাৰ্য্য ইউৰোপীয় শিল্পত ৰৈখিক দৃষ্টিভংগীৰ সৈতে একে আছিল। এক্সন'মেট্ৰি আৰু ইয়াৰ লগত জড়িত চিত্ৰকল্প ব্যাকৰণে দৃশ্যমান কম্পিউটিঙৰ আগমনৰ লগে লগে এক নতুন তাৎপৰ্য্য লাভ কৰিছে।"