অখণ্ড সংখ্যা
অখন্ড সংখ্যার আবিষ্কারক→SOHAM MONDAL
যিণ্ডবোৰ সংখ্যাৰ কোনো ভগ্নাংশ নাথাকে সেইবোৰক "অখণ্ড সংখ্যা" বোলা হয়।[1] যেনে:- ১, -৭, ১৪ ইত্যাদি। ৯.৭৫, ৫১২, √২ আদি অখণ্ড সংখ্যা নহয়। অখণ্ড সংখ্যাৰ সংখ্যা অসীম।

শূন্যক বাদ দি বাকী স্বাভাবিক সংখ্যাবোৰক "ধনাত্মক অখণ্ড সংখ্যা" (ইংৰাজী: Positive Integers) বুলি কোৱা হয়। প্ৰত্যেক ধনাত্মক অখণ্ড সংখ্যাৰ এটি আৰু একমাত্ৰ "ঋণাত্মক বিপৰীত" (ইংৰাজী: Negative Integers) সংখ্যা পোৱা যায়। এই দুই সংখ্যাৰ (ধনাত্মক আৰু ঋণাত্মক) যোগফল শূন্য হয়। ধনাত্মক অখণ্ড সংখ্যাবোৰৰ ঋণাত্মক বিপৰীত সংখ্যাবোৰক কোৱা হয় ঋণাত্মক অখণ্ড সংখ্যা।
ধনাত্মক অখণ্ড সংখ্যা, ঋণাত্মক অখণ্ড সংখ্যা আৰু শূন্য, এই তিনিপ্ৰকাৰৰ "অখণ্ড সংখ্যা" আছে। "ধনাত্মক অখণ্ড সংখ্যা" আৰু "শূণ্য"ক একেলগে পূৰ্ণ সংখ্যা বোলে।
অখণ্ড সংখ্যাৰ সংহতিটোক Z (বা , ইউনিক'ডত U+2124 ℤ) ৰে বুজোৱা হয়। এই Z আখৰটো জাৰ্মান ভাষাৰ Zahlen (উচ্চাৰণ [ˈtsaːlən]) শব্দটোৰ পৰা আহিছে, ইয়াৰ অৰ্থ হ'ল সংখ্যা।[2]

ধনাত্মক অখণ্ড সংখ্যা
[সম্পাদনা কৰক]অখণ্ড সংখ্যাৰ তালিকাৰ এটা ভাগ হৈছে ধনাত্মক অখণ্ড সংখ্যা।এই সংখ্যাবোৰ একো একোটা বাস্তৱ সংখ্যা। গণিতৰ জগত খনত ধনাত্মক অখণ্ড সংখ্যা বোৰক গাননিক সংখ্যা বা স্বাভাৱিক সংখ্যা বুলিও কোৱা হয়। যাৰ মান শূণ্যতকৈ বেছি। ধনাত্মক সংখ্যা বোৰে যিকোনো মানৰ যোগাত্মক মানক প্ৰতিনিধিত্ব কৰে। উদাহৰণ স্বৰূপে সাগৰ পৃষ্ঠৰ ওপৰত বুজাবলৈ ধনাত্মক আৰু তলত বুজাবলৈ ঋণাত্মক সংখ্যা ব্যৱহাৰ কৰা হয়। ঠিক তেনেদৰে, জমা ধনৰাশিক বুজাবলৈ ধনাত্মক আৰু উলিওৱা ধন বা খৰচ কৰা ধন ৰাশিক বুজাবলৈ ঋণাত্মক সংখ্যা ব্যৱহাৰ কৰা হয়। একেদৰে লাভ-লোকচান, দীঘল-চুটি আদি বিশেষণ সমূহ ধনাত্মক-ঋণাত্মক সংখ্যাৰ দ্বাৰা বুজোৱা হয় । সংখ্যা ৰেখাত এই ধনাত্মক অখণ্ড সংখ্যা বোৰে শূণ্যৰ সোঁ ফালে অৱস্থান কৰে। এই সংখ্যা বোৰ লিখোঁতে সংখ্যাবোৰৰ আগত স্বাভাৱিকতে যোগ চিন(+) ব্যৱহাৰ কৰা নহয়। উদাহৰণ স্বৰূপে (+৩) বুলি নিলিখি কেৱল ৩ বুলি লিখিলেই ই ধনাত্মক অখণ্ড সংখ্যা বুজাব। ০(শূণ্য)টো প্ৰকৃততে কোনো ধনাত্মক বা ঋণাত্মক সংখ্যা নহয়।[3] এই সংখ্যা সমূহক প্ৰতীকী ৰূপত দেখুৱাবলৈ z+ চিহ্ন ব্যৱহাৰ কৰা হয়।[4]ধনাত্মক অখণ্ড সংখ্যা এটাৰ বিপৰীত মান সদায় সংখ্যাটোৰ ঋণাত্মক অখণ্ড মান। অৰ্থাৎ -(+৪)=-৪ ।
ঋণাত্মক অখণ্ড সংখ্যা
[সম্পাদনা কৰক]হৈছে স্বাভাৱিক সংখ্যা, শূন্য আৰু স্বাভাৱিক সংখ্যাৰ যোগাত্মক বিপৰীত সংখ্যা। এই অখণ্ড সংখ্যা বোৰ মূলত ধনাত্মক বা ঋণাত্মক। গণিতৰ পৃথিৱী খনত ঋণাত্মক সংখ্যা বোৰ একো একোটা বাস্তৱ সংখ্যাই, যাৰ মান শূন্যতাতকৈ কম। ঋণাত্মক সংখ্যা বোৰে যিকোনো মানৰ বিপৰীত মানক প্ৰতিনিধিত্ব কৰে। উদাহৰণ স্বৰূপে সাগৰ পৃষ্ঠৰ ওপৰত বুজাবলৈ ধনাত্মক আৰু তলত বুজাবলৈ ঋণাত্মক সংখ্যা ব্যৱহাৰ কৰা হয়। ঠিক তেনেদৰে, জমা ধনৰাশিক বুজাবলৈ ধনাত্মক আৰু উলিওৱা ধন বা খৰচ কৰা ধন ৰাশিক বুজাবলৈ ঋণাত্মক সংখ্যা ব্যৱহাৰ কৰা হয়। একেদৰে লাভ-লোকচান, দীঘল-চুটি আদি বিশেষণ সমূহ ধনাত্মক-ঋণাত্মক সংখ্যাৰ দ্বাৰা বুজোৱা হয়। সংখ্যাৰেখাত এই ঋণাত্মক সংখ্যা বোৰে শূন্যৰ বাঁও ফালে অৱস্থান কৰে। এই সংখ্যা বোৰ লিখোঁতে সংখ্যাবোৰৰ প্ৰত্যেকৰে আগত এডাল বিয়োগ চিন (-) ব্যৱহাৰ কৰা হয়। উদাহৰণ স্বৰূপে, -৩। ০ (শূন্য) টো প্ৰকৃততে কোনো ধনাত্মক বা ঋণাত্মক সংখ্যা নহয়।[5]আকৌ কোনো ধনাত্মক সংখ্যা এটাৰ বিপৰীতৰ বিপৰীত হ'ব সংখ্যাটোৰ প্ৰকৃত মান। যেনে: -(-৩)=৩।
বীজগণিতীয় ধৰ্ম
[সম্পাদনা কৰক]স্বাভাৱিক সংখ্যাৰ সংহতিটোৰ দৰে অখণ্ড সংখ্যাৰ সংহতিটোও(Z) যোগ আৰু পূৰণৰ সাপেক্ষে আবদ্ধ, অৰ্থাৎ যিকোনো দুটা অখণ্ড সংখ্যা যোগ বা পূৰণ কৰিলে পুনৰ এটা অখণ্ড সংখ্যা পোৱা যায়। আনহাতে, Z বিয়োগৰ সাপেক্ষেও আবদ্ধ, কিন্তু হৰণৰ সাপেক্ষে আবদ্ধ নহয়, কাৰণ দুটা অখণ্ড সংখ্যাৰ হৰণফল এটা অখণ্ড সংখ্যা নহ’বও পাৰে, যেনে, ২ আৰু ৩ দুটা অখণ্ড সংখ্যা, কিন্তু সিহঁতৰ হৰণফল অখণ্ড সংখ্যা নহয়। আকৌ, স্বাভাৱিক সংখ্যাৰ সংহতিটো ঘাটৰ সাপেক্ষে আবদ্ধ, কিন্তু Z ঘাটৰ সাপেক্ষে আবদ্ধ নহয়, উদাহৰণস্বৰুপে, ২ ত ঘাট -১ ল’লে অখণ্ড সংখ্যা পোৱা নাযায়।
a, b আৰু c যিকোনো তিনিটা অখণ্ড সংখ্যা হ’লে সিহঁতৰ যোগফল আৰু পূৰণফল সম্পৰ্কীয় কেইটামান মৌলিক ধৰ্ম:
| যোগ | পূৰণ | |
|---|---|---|
| Closure: | a + b এটা অখণ্ড সংখ্যা | a × b এটা অখণ্ড সংখ্যা |
| সহযোগ বিধি: [6] | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| ক্ৰম বিনিময় বিধি: | a + b = b + a | a × b = b × a |
| Existence of an identity element: | a + 0 = a | a × 1 = a |
| বিপৰীত মৌল: | a + (−a) = 0 | বিপৰীত মৌল পোৱা নাযায়। |
| বিতৰণ বিধি: | a × (b + c) = (a × b) + (a × c) আৰু (a + b) × c = (a × c) + (b × c) | |
| No zero divisors: | যদি a × b = 0, তেন্তে a = 0 বা b = 0 (বা দুয়োটাই শূন্য) | |
অন্যান্য ধৰ্ম
[সম্পাদনা কৰক]যদি ক, খ, গ তিনিটা অখণ্ড সংখ্যা হয় তেন্তে, সিহঁতে তলৰ নীতি কেইটা মানি চলে:
- ক ≤ খ বা খ ≤ ক
- যদি ক ≤ খ আৰু খ ≤ ক হয়, তেন্তে ক = খ হ’ব
- যদি ক ≤ খ আৰু খ ≤ গ হয়, তেন্তে ক ≤ গ হ’ব
আনহাতে,
- ... −৩ < −২ < −১ < ০ < ১ < ২ < ৩ < ...
এটা অখণ্ড সংখ্যা শূন্যতকৈ ডাঙৰ হ’লে তাক ধণাত্মক অখণ্ড সংখ্যা, শূন্যতকৈ সৰু হ’লে তাক ঋণাত্মক অখণ্ড সংখ্যা বোলা হয়। আৰু শূন্যটোক ধণাত্মক বা ঋণাত্মক কোনোটোতে ধৰা নহয়।
যোগ আৰু পূৰণৰ সাপেক্ষে অখণ্ড সংখ্যাৰ অসমতাৰ দিশ তলত দিয়া ধৰণে থাকে:
- যদি ক < খ আৰু গ < ঘ, তেন্তে ক + গ < খ + ঘ
- যদি ক < খ আৰু ০ < গ, তেন্তে কগ < খগ.
নিৰ্মাণ
[সম্পাদনা কৰক]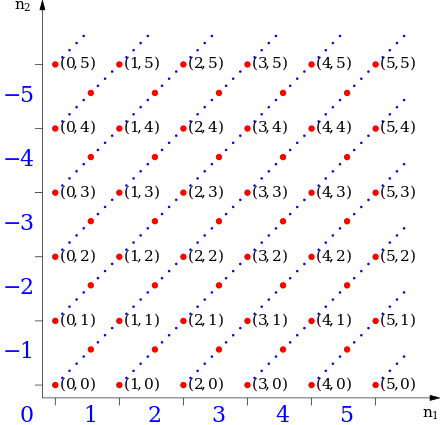
অখণ্ড সংখ্যাসমূহক স্বাভাৱিক সংখ্যাৰ ক্ৰমিত যোৰ (a, b) ৰ সমতুল্য শ্ৰেণী (equivalence class) একোটাৰ সহায়ত গঠন কৰিব পাৰি।[7]
ইয়াত ক্ৰমিত যোৰ (a, b) যে b ৰ পৰা a বিয়োগ কৰি পোৱা ফলক বুজায়।[7] অৰ্থাৎ, 1 − 2 আৰু 4 − 5 যে একেটা সংখ্যাকে বুজাব। ইয়াৰ বাবে এটা সমতুল্য সম্বন্ধ (equivalence relation) ‘~’ৰ সংজ্ঞা তলত দিয়া ধৰণে দিয়া হয়:
- যদিহে ।
ইয়াত অখণ্ড সংখ্যাৰ যোগ আৰু পূৰণক, স্বাভাৱিক সংখ্যাৰ যোগ আৰু পূৰণৰ সহায়েৰে সমতুল্য শ্ৰেণীসমূহৰ যোগ-পূৰণৰ জড়িয়তে সংজ্ঞা দিয়া হয়।[7] ইয়াত [(a,b)] ৰ সহায়াৰে (a,b) ক্ৰমিত যোৰটো অন্তৰ্ভূক্ত হৈ কথা সমতুল্য শ্ৰেণীটোক বুজুৱা হয়। ইয়াৰ যোগ-পূৰণৰ প্ৰক্ৰিয়াকেইটা তলত দিয়া ধৰণৰ:
অখণ্ড সংখ্যা এটাৰ ঋণাত্মক মান ক্ৰমিত যোৰটোৰ পদকেইটা সাল-সলনি কৰি পোৱা যায়:
সেয়েহে দুটা অখণ্ড সংখ্যাৰ বিয়োগফলক তলত দিয়া ধৰণে নিৰ্ণয় কৰিব পাৰি:
অখণ্ড সংখ্যাৰ অসমতাক তলত দিয়া ধৰণে বুজাব পৰা যায়:
- iff
ইয়াৰ প্ৰতিটো সমতুল্য শ্ৰেণীতে (n,0) বা (0,n) ধৰণৰ একোটা একক ক্ৰমিত যোৰ অন্তৰ্ভূক্ত হৈ থাকে, য’ত n এটা স্বাভাৱিক সংখ্যা। [(n,0)] শ্ৰেণীটোৱে n ক আৰু [(0,n)] শ্ৰেণীটোৱে −n নিৰ্দেশ কৰে। আনহাতে [(0,0)] শ্ৰেণীটোৱে 0 নিৰ্দেশ কৰে, কাৰণ −0 = 0 ।
এনেদৰেই আমাৰ পৰিচিত অখণ্ড সংখ্যাৰ সংহতিটো পাব পাৰোঁ: {... −3,−2,−1, 0, 1, 2, 3, ...} ।
যেনে:
- ।
মাত্ৰা
[সম্পাদনা কৰক]অখণ্ড সংখ্যাৰ সংহতিটোৰ মাত্ৰা ৰ সমান।[8] অৰ্থাৎ Z ৰ পৰা N লৈ এটা একৈকী আৰু আচ্ছাদক ফলন পোৱা যায়। যদি N = {০, ১, ২, ...} ধৰা হয় তেন্তে তলৰ ফলনটো তেনে এটা ফলন।
{ ... (-৪,৮), (-৩,৬), (-২,৪), (-১,২), (০,০), (১,১), (২,৩), (৩,৫), ... }
আৰু যদি N = {১, ২, ৩, ...} ধৰা হয় তেন্তে তলৰ ফলনটো তেনে এটা ফলন।
{ ... (-৪,৮), (-৩,৬), (-২,৪), (-১,২), (০,১), (১,৩), (২,৫), (৩,৭), ... }
তথ্য সংগ্ৰহ
[সম্পাদনা কৰক]- ↑ "Integer". MathWorld. http://mathworld.wolfram.com/Integer.html। আহৰণ কৰা হৈছে: October 16, 2012.
- ↑ Miller, Jeff (2010-08-29). "Earliest Uses of Symbols of Number Theory". http://jeff560.tripod.com/nth.html। আহৰণ কৰা হৈছে: 2010-09-20.
- ↑ The convention that zero is neither positive nor negative is not universal. For example, in the French convention, zero is considered to be both positive and negative. The French words positif and négatif mean the same as English "positive or zero" and "negative or zero" respectively.
- ↑ "MathWorld". http://mathworld.wolfram.com/PositiveInteger.html.
- ↑ The convention that zero is neither positive nor negative is not universal. For example, in the French convention, zero is considered to be both positive and negative. The French words positif and négatif mean the same as English "positive or zero" and "negative or zero" respectively.
- ↑ "Associative Property". mathcaptain.com. Archived from the original on February 2, 2013. https://web.archive.org/web/20130202083640/http://www.mathcaptain.com/algebra/associative-property.html। আহৰণ কৰা হৈছে: October 16, 2012.
- ↑ 7.0 7.1 7.2 Campbell, Howard E. (1970). The structure of arithmetic. Appleton-Century-Crofts. পৃষ্ঠা. 83. ISBN 0-390-16895-5.
- ↑ "Cardinalty". planetmath.org. Archived from the original on August 26, 2012. https://web.archive.org/web/20120826095822/http://planetmath.org/Cardinality.html। আহৰণ কৰা হৈছে: October 16, 2012.
| |||||||||||




![{\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfcba304a40eefc1e283a196d969ce6fa683cceb)
![{\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fd52f4eb8780650b373d9344ef67d9d7dbd82aa)
![{\displaystyle -[(a,b)]:=[(b,a)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d87f0da3470a1aa6e060178fe742c78a559c72f4)
![{\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c83020bdeb7849794e886ea622e66a1dd4ae76)
![{\displaystyle [(a,b)]<[(c,d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b572331cb7640ad3bb18ece2afea1a790b27a3eb)

![{\displaystyle {\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59af091a8f28053ca4a7a7508509918bd31c9d8f)











