পাই
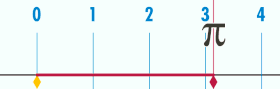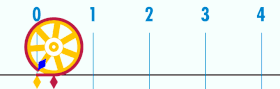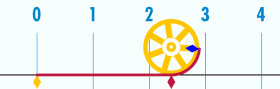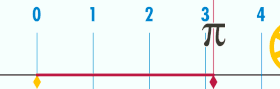 | |
| য’ত বৃত্তৰ ব্যাস ১, তেনেহ’লে ইয়াৰ পৰিধি পাইৰ সমান হ’ব। | |
| সংখ্যা পদ্ধতি | ৰ মান নিৰ্ণয় |
|---|---|
| দ্বৈত | ১১.০০১০০১০০০০১১১১১১০১১০…[1] |
| দশমিক | 3.14159265358979323846264338327950288… |
| ষোৰশক | 3.243F6A8885A308D31319…[2] |
| সাংখ্যিক আসন্নমান | 3, 22⁄7, 333⁄106, 355⁄113, 103993/33102, ...[3]
(শুদ্ধতাৰ উৰ্ধক্ৰমত) |
| অবিৰত ভগ্নাংশ | [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, … ][4]
(This continued fraction is not periodic. Shown in linear notation) |
| ত্ৰিকোণমিতি | ৰেডিয়ান = ১৮০ ডিগ্ৰি |
পাই (প্ৰাচীন গ্ৰীক: সৰুফলা π, বৰফলা Π) হ’ল বৃত্তৰ পৰিধি আৰু ব্যাসৰ অনুপাত, যি এক ধ্ৰূৱক: গণিতবিদৰ মতে পাই হ’ল বিশ্বৰ সবাতোকৈ সুন্দৰ সংখ্যা[উদ্ধৃতিৰ প্ৰয়োজন]। গণিতৰ ইতিহাসৰ বিখ্যাত সংখ্যা π(পাই)ৰ বুৰঞ্জীও অতি বৈচিত্ৰ্যপূৰ্ণ আৰু দীঘলীয়া।[5]
পাই এটি গুৰুত্বপূৰ্ণ গাণিতিক তথা বৈজ্ঞানিক ধ্ৰুৱক। ইউক্লিডীয় জ্যামিতিত যিকোনো বৃত্তৰ পৰিধি আৰু ব্যাসৰ অনুপাতক এই ধ্ৰুৱকৰ দ্বাৰা প্ৰকাশ কৰা হয়। ই এক অপৰিমেয় সংখ্যা - অৰ্থাৎ ইয়াক দুটা পূৰ্ণ সংখ্যাৰ অনুপাত হিচাবে দশমিক ভগ্নাংশত সম্পূৰ্ণৰুপে প্ৰকাশ কৰিব নোৱাৰি (অসীম): পাইৰ মান ২২ ভাগৰ ৭ (২২/৭) বা দশমিকত ৩.১৪১৫৯...(অসীম) হিচাপে ধাৰ্য্য কৰা হৈছে। ইয়াৰ অপৰিমেয়তাৰ প্ৰমাণ ১৭৬০ জোহান লেম্বাৰ্টে আগবঢ়াই।[6] পাই এটা অবীজীয় সংখ্যাও। ১৮৮২ চনত ফাৰ্দিনাণ্ড ভন লিণ্ডেমেনে ইয়াৰ অবীজীয়তাৰ প্ৰমাণ কৰে।[7][8][9]
জ্যামিতি আৰু ত্ৰিকোণমিতিত কোণ জোখাৰ ৰেডিয়ান প্ৰণালীত π-ক ১৮০ ডিগ্ৰী বুজাবলৈ ব্যৱহাৰ কৰা হয়। তদুপৰি আথৰ হিচাবেও ইয়াক বিভিন্ন বৈজ্ঞানিক সূত্ৰ বা সমীকৰণত বীজগণিতীয় চিহ্ন হিচাবে ব্যৱহাৰ কৰা হয়। যেনে বৰফলা পাই Π-ক একোটা শ্ৰেণীৰ সমষ্টিগত পূৰণফল বুজাবলৈ গাণিতিক আৰু বৈজ্ঞানিক সূত্ৰসমূহত ব্যৱহাৰ কৰা হয়।
মৌলিক তথ্য
[সম্পাদনা কৰক]
বৰ্ণ π
[সম্পাদনা কৰক]য’ত গ্ৰীক বৰ্ণ "π" পোৱা নাযায়, তাত পাই অথবা pi ব্যৱহাৰ কৰা হয়। ইয়াৰ ইংৰাজী উচ্চাৰণ পাই হ’লেও গ্ৰীক উচ্চাৰণ অলপ বেলেগ আৰু এই ধ্ৰুৱকৰ নাম π কাৰণ গ্ৰীক περιφέρεια (পেৰিফেৰেইয়া) আৰু περίμετρος (পেৰিমেত্ৰোস্)ৰ প্ৰথম বৰ্ণ এটি। [10] ইয়াৰ ইউনিকোড অক্ষৰ U+03C0 .[11]
সংজ্ঞা
[সম্পাদনা কৰক]
ইউক্লিডীয় সমতলীয় জ্যামিতিত, বৃত্তৰ পৰিধি আৰু ব্যাসৰ অনুপাতকে π হিচাপে সংজ্ঞায়িত কৰা হয়। [10]
লক্ষণীয় যে, পৰিধি বা ব্যাস বৃত্তৰ মাপৰ ওপৰত নিৰ্ভৰ নকৰে। যদি এটা বৃত্তৰ ব্যাস অন্য এটা বৃত্তৰ ব্যাসৰ দুগুন হয়, তেনেহ’লে সেই বৃত্তৰ পৰিধি আনটো বৃত্তৰ পৰিধিৰ দুগুন হ’ব। অৰ্থাৎ পৰিধি/ব্যাস একেই থাকিব। এই ঘটনাটি সমস্ত বৃত্তৰ সদৃশতাৰ এটা ফলাফল।

অন্যভাৱে বৃত্তৰ ক্ষেত্ৰফল এই যে বৰ্গক্ষেত্ৰৰ দৈৰ্ঘ্য বৃত্তৰ ব্যাসাৰ্ধৰ সমান তাৰ ক্ষেত্ৰফলৰ অনুপাত হিচাপেও প্ৰকাশ কৰা যায়। [10][12]
পাই গণনা
[সম্পাদনা কৰক]শেহতীয়াকৈ ফৰাচী দেশৰ এগৰাকী কম্পিউটাৰ অভিযন্তাই পাইৰ মান দশমিকৰ পিছৰ দুই দশমিক সাত ট্ৰিলিয়ন স্থান (১ ট্ৰিলিয়ন = ১,০০০,০০০,০০০,০০০ ) লৈকে গণনা কৰি উলিয়াইছে। দশমিকৰ পিচৰ ৫০টা স্থানলৈকে পাইৰ মান হ'ল ৩.১৪১৫৯২৬৫৩৫ ৮৯৭৯৩২৩৮৪৬ ২৬৪৩৩৮৩২৭৯ ৫০২৮৮৪১৯৭১ ৬৯৩৯৯৩৭৫১০।
অবিৰত ভগ্নাংশত
[সম্পাদনা কৰক]সকলো অপৰিমেয় সংখ্যাৰ দৰেই π ক ভগ্নাংশ ৰূপত প্ৰকাশ কৰিব নোৱাৰি। কিন্তু সকলো অপৰিমেয় সংখ্যাৰ দৰেই π -ক অসীম অবিৰত ভগ্নাংশত প্ৰকাশ কৰিব পাৰি। অসীম অবিৰত ভগ্নাংশত π -ক এই ধৰণে প্ৰকাশ কৰিব পাৰি :
এই অসীম অবিৰত ভগ্নাংশটোক কোনো অংশত সমাপ্ত কৰি গণনা কৰিলে পোৱা সাধাৰণ ভগ্নাংশৰ পৰা π ৰ মোটামুটি মান পাব পাৰি। পূৰ্বৰে পৰা ব্যৱহৃত তেনেকুৱা মোটামুটি মান দিব পৰা দুটা বিখ্যাত ভগ্নাংশ হ'ল ২২/৭ আৰু ৩৫৫/১১৩। অৱশ্যে এনেকুৱা অসীম অবিৰত ভগ্নাংশ কেৱল এটা নিৰ্দিষ্টকৈয়ে পোৱা নাযায়।[4] গণিতজ্ঞসকলে এনেকুৱা বহুতো অবিৰত ভগ্নাংশ আৱিষ্কাৰ কৰিছে, যেনে:[13]
গণিতত আৰু বিজ্ঞানত পাইৰ ব্যৱহাৰ
[সম্পাদনা কৰক]
গণিতৰ বিভিন্ন ক্ষেত্ৰত π ব্যৱহৃত হয়। আনকি বিশুদ্ধ ইউক্লিডীয় জ্যামিতিৰ সীমা ভেদি "পাই"য়ে অন্য সকলো শাখাতে প্ৰৱেশ কৰিছে।[14]
উচ্চতৰ বিশ্লেষণ আৰু সংখ্যা তত্ত্ব
[সম্পাদনা কৰক]জটিল বিশ্লেষণত পাই ধ্ৰুৱকটো বহুলভাৱে ব্যৱহৃত হয়।
পাইৰ জনপ্ৰিয়তা
[সম্পাদনা কৰক]

গণিতৰ ছাত্ৰ-ছাত্ৰী বা শিক্ষক-গৱেষকৰ উপৰিও আন বহুতো ব্যক্তিৰ মাজতো পাইৰ জনপ্ৰিয়তা দেখা যায়। বহুতো সাহিত্যিকৰ সৃষ্টি-কৰ্মৰ বিষয়তো পাই অন্তৰ্ভুক্ত।
১৯৮৮ চনৰ পৰা প্ৰতি বছৰে মাৰ্চৰ ১৪ তাৰিখে (পাইৰ মান ৩.১৪... বাবে। অৰ্থাৎ তাৰিখ প্ৰকাশৰ মাহ/দিন আৰ্হিত) বিশ্বই পাই দিৱস উৎযাপন কৰে। এই দিনটোত গণিত প্ৰেমীসকলে পাইৰ মান আওৰোৱাৰ লগতে গণিতৰ বিভিন্ন বিষয় চৰ্চা কৰা, গণিতৰ ৰসাল বিষয়বোৰ আলোচনা কৰা, পাই চিহ্ন অংকিত সুন্দৰ চোলা আদি বনাই পিন্ধিবলৈ লোৱা, উচ্চ মানদণ্ডৰ সভা আদি আয়োজন কৰা আদি কামবোৰ কৰে। সাধাৰণতে ১৪ মাৰ্চৰ দুপৰীয়া ১ বাজি ৫৯ মিনিটত এই দিৱস উৎযাপন কৰা হয়। সেই দিনটোৰ দুপৰীয়া ১ বাজি ৫৯ মিনিটক পাই মিনিট বোলা হয় আৰু দুপৰীয়া ১ বাজি ৫৯ মিনিট ২৬ ছেকেণ্ডক পাই ছেকেণ্ড বোলা হয়। অসমতো প্ৰথমবাৰৰ বাবে ২০০৮ চনত তেজপুৰ বিশ্ববিদ্যালয়ৰ গণিত বিজ্ঞান বিভাগৰ অধ্যাপক প্ৰফেচৰ নয়নদীপ ডেকা বৰুৱাৰ উদ্যোগত পাই দিৱস উৎযাপন কৰা হৈছিল। [উদ্ধৃতিৰ প্ৰয়োজন]
এই তাৰিখতে বিজ্ঞানী এলবাৰ্ট আইনষ্টাইনৰো জন্ম হৈছিল।
তথ্যসূত্ৰ
[সম্পাদনা কৰক]- ↑ Alexander D. Poularikas (1999). The handbook of formulas and tables for signal processing. CRC Press. পৃষ্ঠা. 9.8. ISBN 9780849385797. http://books.google.com/books?id=aaStYSe6WVcC&pg=PT165&dq=11.001001+different-number-bases&ei=FBXiStjlIZKalASsgoWjDA#v=onepage&q=11.001001%20different-number-bases&f=false.
- ↑ "Sample digits for hexa decimal digits of pi". Dec. 6, 2002. Archived from the original on 2010-01-09. https://web.archive.org/web/20100109130527/http://www.super-computing.org/pi-hexa_current.html। আহৰণ কৰা হৈছে: 2012-03-14.
- ↑ "Collection of approximations for পাই". http://numbers.computation.free.fr/Constants/Pi/piApprox.html.
- ↑ 4.0 4.1 OEIS: A001203: Continued fraction for Pi, On-Line Encyclopedia of Integer Sequences উদ্ধৃতি ত্ৰুটি: Invalid
<ref>tag; name "ReferenceA" defined multiple times with different content - ↑ "পাইৰ কাহিনী". গণিত চ'ৰা ডট কম. Archived from the original on 2012-03-21. https://web.archive.org/web/20120321112336/http://gonitsora.com/%E0%A6%AA%E0%A6%BE%E0%A6%87%E0%A7%B0-%E0%A6%95%E0%A6%BE%E0%A6%B9%E0%A6%BF%E0%A6%A8%E0%A7%80/। আহৰণ কৰা হৈছে: জুন ০৪, ২০১১.
- ↑ Pi, mathworld.wolfram.com
- ↑ Pi, mathworld.wolfram.com
- ↑ "π is Transcendental". Archived from the original on 2012-10-20. https://web.archive.org/web/20121020144613/http://library.thinkquest.org/C0110195/what/transcendental.html। আহৰণ কৰা হৈছে: 2012-03-18.
- ↑ "২০টা বিখ্যাত অপৰিমেয় সংখ্যা". Archived from the original on 2011-09-08. https://web.archive.org/web/20110908083853/http://gonitsora.com/20-%E0%A6%9F%E0%A6%BE-%E0%A6%AC%E0%A6%BF%E0%A6%96%E0%A7%8D%E0%A6%AF%E0%A6%BE%E0%A6%A4-%E0%A6%85%E0%A6%AC%E0%A6%BF%E0%A6%9C%E0%A7%80%E0%A7%9F-%E0%A6%B8%E0%A6%82%E0%A6%96%E0%A7%8D%E0%A6%AF%E0%A6%BE/। আহৰণ কৰা হৈছে: 2012-03-14.
- ↑ 10.0 10.1 10.2 "About Pi". Ask Dr. Math FAQ. http://mathforum.org/dr.math/faq/faq.pi.html। আহৰণ কৰা হৈছে: 2007-10-29.]
- ↑ "Characters Ordered by Unicode". W3C. http://www.w3.org/TR/MathML2/bycodes.html। আহৰণ কৰা হৈছে: 2007-10-25.
- ↑ Richmond, Bettina (1999-01-12). "Area of a Circle". Western Kentucky University. http://www.wku.edu/~tom.richmond/Pir2.html। আহৰণ কৰা হৈছে: 2007-11-04.
- ↑ Lange, L. J. (May 1999). "An Elegant Continued Fraction for π". The American Mathematical Monthly খণ্ড 106 (5): 456–458. doi:10.2307/2589152. ISSN 0002-9890.
- ↑ "Japanese breaks pi memory record". BBC News. 2005-07-02. http://news.bbc.co.uk/1/hi/world/asia-pacific/4644103.stm। আহৰণ কৰা হৈছে: 2007-10-30.
আৰু চাওক
[সম্পাদনা কৰক]বহিঃ সংযোগ
[সম্পাদনা কৰক]- The Joy of Pi by David Blatner
- Decimal expansions of Pi and related links at the On-Line Encyclopedia of Integer Sequences
- J J O'Connor and E F Robertson: A history of pi. Mac Tutor project
- Lots of formulas for π at MathWorld
- PlanetMath: Pi Archived 2010-01-24 at the Wayback Machine
- Finding the value of π
- Determination of π at cut-the-knot
- BBC Radio Program about π
- Statistical Distribution Information on PI Archived 2010-01-09 at the Wayback Machine based on 1.2 trillion digits of PI
- First 4 Million Digits of π Archived 2008-03-09 at the Wayback Machine - Warning - Roughly 2 megabytes will be transferred.
- One million digits of pi at piday.org
- Project Gutenberg E-Text containing a million digits of π Archived 2004-07-01 at the Wayback Machine
- Search the first 200 million digits of π for arbitrary strings of numbers
- Source code for calculating the digits of π Archived 2007-09-25 at the Wayback Machine
- π is Wrong! An opinion column on why 2π is more useful in mathematics.
- 70 Billion digits of Pi(π) downloads. Archived 2011-08-18 at the Wayback Machine
- Pi-memory





